The black body
If you heat a metal bar, you will note that it emits rays ranging from red to violet. This raises the question of how to formulate the frequency of this radiation as a function of its temperature. In order to capture the rays better, the idea of heating a hollow body was originated. Thus, the radiation emitted remains inside and, by allowing it to pass through a small hole, it becomes easy to carry out measurements. Formulas were developed, but none of them matched the experiment. In the early 20th century, Max Planck decided to tackle this problem.
Note that the name “black body” is due to the fact that the radiation emitted was practically absorbed by the internal wall.
The black body is a sound box that enables you to obtain all the harmonies of the fundamental frequency. If f is the frequency and df is an infinitesimal variation in this frequency, and if V is the volume of the cavity, it is calculated that the number of frequencies between f and f + df equals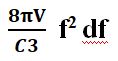
Planck knew of Boltzmann’s theory, which he was not a follower of. In a volume of gas consisting of a large number of molecules, the mean energy Em of a molecule statistically equals kT. T is the temperature in relation to absolute zero and k is what is known as Boltzmann’s constant. If you consider the system as a whole, there is an equipartition of Em = kt
The energy is distributed equitably over a large number of small, independent parts, provided that it is also in a state of thermal equilibrium. If E is that small part, the probability, according to Boltzmann, of it having a thermal equilibrium is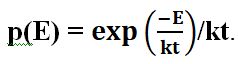
It consists of a stationary wave in the black body’s spectrum.
This is Newton’s well-known experiment.
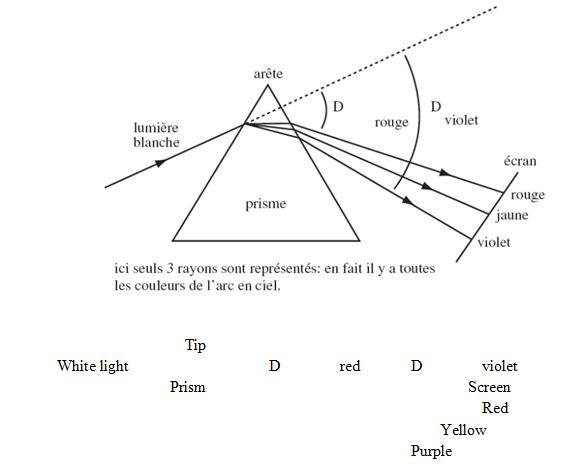
Here, only 3 rays are represented: in fact, all the colours of the rainbow are involved
Passing through the prism, the light is, in a way, spread between various wavelengths that represent the colours that our sensory perceptions can pick up. This idea of spectral dispersion will also be encountered in the case of Schrödinger’s wave function.
The curves obtained from the intensity of the radiation as a function of the wavelength are indicated opposite. It should be noted that there is a maximum, like there is for a bell curve. This maximum deviates to the left as the intensity increases. The curves flatten out if the temperature drops. This means that the bits of energy end up accumulating around 0°k. This is Bose-Einstein condensation.
Max Planck’s intellectual approach is based on formulas already found before his day, but which were inadequate. It is also based on Boltzmann’s statistics.
Max Planck thought that the inside of the hollow body featured a large number of harmonic oscillators that are simply springs, on the end of which an electric charge is suspended, like that of an electron. This was a good image for the behaviour of the atom that Max Planck did not yet know. Using these data, he came up with a formula. It adopted the formula already indicated of 
where N(f) is the number of frequencies in the interval df namely: 
It should be noted that the last expression is the one used in Bose-Einstein distribution.
Planck then came up with a hypothesis whereby the coefficient h of the frequency f cannot vary. It has a set value which is 6.6 x 10-34 joules/second. In other words, there can be no derivation of this coefficient because, in that event, it would fall back into the old formulas. With his hypothesis regarding harmonic oscillators, he was forced to admit that the electric charge can only oscillate by inputting well-defined energy. As he neither believed in atoms nor in the discontinuity of energy, this was a major disappointment for him.
With the photo-electric effect, Einstein would come to overturn all that. As a matter of fact, he noted that you can unstick an electron from the metal only if, instead of increasing the luminous intensity, you opt to use a higher frequency. As Max Planck had drawn up his formula using Boltzmann’s statistics, which only apply to molecules, he had to admit that light also consisted of energy particles hf.
This is how photons, whose name would be established later, came to be born.
Then came the Indian genius Bose who went back to Planck’s formula whilst considering light to be a gas consisting of photons.
We do have a formal proof for the black body. This is the Universe itself. Indeed, 380,000 years after the Big Bang, the radiation involved has become disconnected from matter. It has become dispersed throughout Creation due to expansion. Its current temperature is approximately 3 degrees Kelvin.
Planck’s formula was thus confirmed in no uncertain terms. It is extraordinary that you can prove Planck’s constant h on the scale of the Universe itself. The consequence of Planck’s setback was establishing this very low action value, which however is not nil.
If the action had been continuous, as Planck wanted it to be, the temperature of the Universe would have been infinite! Life would not have been able to develop.
This extraordinary discovery by Planck, supplemented by Einstein, came to be the starting point for the whole of quantum physics and enabled us to attain in-depth knowledge of the behaviour of quantum objects at microscopic level.
Related Posts
-
Fluctuations
Posted on 13 Juin 2019
-
The Wave-Corpuscle duality
Posted on 27 Mai 2019
-
HYDROGEN
Posted on 20 Mai 2019
-
Anaximander, circa 555 BC
Posted on 13 Mai 2019
Tags
Share This
