The Wave-Corpuscle duality

27 Mai 2019 by René Lebon

Louis de Broglie, the prince of dualism (1892-1987)

In a thesis presented at the Sorbonne in 1924, Louis de Broglie put forward the following hypothesis: “Centuries of discussions have not managed to bring an end to the alternative of considering light to be either particles or a wave.”

The black body experiment, described elsewhere, showed that, according to Einstein, light could be considered both a wave and a stream of particles, without however settling the debate. If it seemed that could be envisaged for the photon, why could it not be the case for particles with a mass and a charge like the electron? This particle has a movement quantity mv (m is the mass and v is the velocity).

Pushing the analogy with the photon further, Louis de Broglie laid out the equivalency of the energy demonstrated via the black body experiment, namely:

E = hf (h being Planck’s constant and f being the frequency of the photon) the Poincaré-Einstein formula, giving the energy of a mass particle, namely:

E = mc² (with c being the considerable speed of light, which is 10⁸ m/s).

You thereby obtain hf = mc².

If λ is the wavelength and λ = c/f, consequently you obtain h = mc x c/f = mc.λ

You can then admit that this formula is valid for a particle with a speed of v < c. You then get mv = h/λ or mv.λ = h

And what if that was confirmed through experimentation?

This was the case.

In 1927, Davisson and Germer discovered the diffraction of electrons by crystals. This extremely simple formula, as strange as it may seem, is now generally accepted. Louis de Broglie’s idea, which may have seemed crazy, to the contrary turned out to be extremely fruitful.

A wave should only be taken into consideration for microscopic masses. It is also linked to objects the size of an elephant, but in those cases it is not perceptible. It has no physical substance and cannot be shown. It is simply a probability wave.

Louis de Broglie set out his thesis as follows:

“It may be conceived that, owing to a major law of nature, to each piece of energy with a specific mass m, a frequency phenomenon f is linked so that you get:

hf = mc², with f being measured in the system linked to the piece of energy.”

The analogy between the behaviour of a particle that has no mass and a photon and a electron with mass and its movement quantity mv are found in seeking out a least action principle that nature would obey. To demonstrate this, there are two approaches:

Fermat’s approach, which indicates that light, if you consider it to consist of straight rays, follows the path which takes it the least amount of time.
Maupertuis’s approach, which sees action as being the product of movement quantity mv times the distance travelled by minimising it.

Fermat’s geometrical approach works in an environment with a constant refraction index n.

Then came Hamilton, who demonstrated that these two ways of viewing things are similar. Indeed, if you consider light to be spread via waves, as stated in Huygens’ thesis, and that the environment has a refraction index varying gradually, then the wave front turns; it does not remain vertical.

And yet for a mobile mass, the same thing occurs; its trajectory is curved by refraction. From this, it may be concluded that light and matter behave the same way when they both seek the least action.

Based on this observation, Louis de Broglie was then prompted to state the idea that, like light, the mobile mass has a wave that is associated with it.

This occurs in the reference value Ro at rest, where the material particle either does or does not have a pulse of mv = hλ or h/f.

What happens in the case of a reference value R’ that moves at a relative speed of v?

If t is the time measured in Ro, the time t’ marked by the clock for Ro becomes:

In the case of the reference value R’, the wave amplitude is provided by and with t’ that gives you: ①

The amplitude of a wave with a phase speed of v is written as ②

① and ② represent the same phenomenon in R’ and are therefore identical, which takes the form of where v.v = c²

The velocity v of the particle and the phase velocity of the associated wave v are therefore inversely proportional. Should the velocity v be nil, the transmission of the forces is instantaneous. This is the limit case for Newton’s classic mechanics.

The phase velocity corresponds to the wave’s zero transmission velocity. The amplitude of this phase wave is nil and there is no transmission of energy. Its velocity may be higher than c without breaking the rules of relativity in the event that it is the speed of the energy, or in other words v, that is limited to c.

Should the wave be monochromatic, the associated particle cannot be located. But you may see the particle as a packet of waves with frequencies that are very close together. Two phenomena then occur. There is interference between these waves even though they accumulate in the middle of the packet and are destroyed until they cancel out at the ends. There is therefore a limited formation in time and space that may be compared to a particle. As the environment has a constant refraction index, the waves will not have the same speed.

You therefore have to define a group speed vg.

A wave is characterised by its pulse , and the number of waves k.

The velocity vg is the quotient of the variation in due to the corresponding variation in , bearing in mind that and k are linked by the relation which turns out to be the phase velocity v of the related wave.

As each wave carries energy, the speed vg cannot exceed c.

To the contrary, the phase wave associated with the waves packet is a notional wave with a velocity of . It does not transmit energy.

When the waves are superimposed, their energy deployment, characterised by the amplitude and the bulging of the wave, are added together like the frequencies. In other words, the total energy of the waves packet will accumulate in the middle and diminish at the ends. The more waves there are, the more the waves maximum will taper away. The more the packet contains waves subject to the conditions set out above, the more its energy will be concentrated at its maximum.

According to Fourier’s analysis, the waves can be superimposed or, in other words, an accumulation of waves with whole-number frequencies is transformed into a periodic function which creates a peak. The Fourier coefficients that relate to the energy bulges of the overlapping waves build up. The result matches the following diagram:

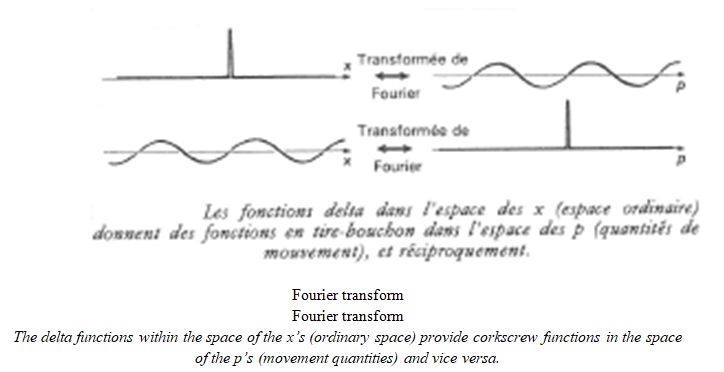
This phenomenon is very important because it does symbolise the wave-particle well. It only becomes possible to locate the particle via the closeness of the waves. If they are more spaced apart, then the location of the energy concentration becomes vague. This is found in inequalities in terms of indeterminacy and the presence probability calculation.

Louis de Broglie’s wave provides confirmation of Bohr’s thesis, according to which the kinetic momentums of the various levels of the electron in a hydrogen atom are quantified. If the level is n, the kinetic momentum is